本文第一作者王涛来自中国人民大学,共同第一作者李梦雨 (https://mengyu8042.github.io/) 来自清华大学。通讯作者为中国人民大学张琼助理教授 (https://sarahqiong.github.io/) 与孟澄助理教授 (https://cheng-bdal.github.io/)。其他作者还包括来自中国人民大学的曾舸舵。
在三维视觉领域,3D Gaussian Splatting (3DGS) 是近年来大热的三维场景建模方法。它通过成千上万的高斯球在空间中“泼洒”,拼合成一个高质量的三维世界,就像是把一片空白的舞台,用彩色的光斑和粒子逐渐铺满,最后呈现出一幅立体的画卷。然而,高斯球冗余一直让3DGS的存储与渲染速度受限。本文提出把 3DGS 看成高斯混合模型,用最优传输视角做全局“简化”。实验显示在仅保留 10% 高斯时,画质几乎不掉、并稳定优于主流压缩方案。

代码地址:
https://github.com/DrunkenPoet/GHAP
论文地址:
https://arxiv.org/abs/2506.09534

要点速览
当前 3DGS 通过数以百万计的各向异性高斯球表示场景,渲染速度快但具有高度的冗余。现有 3DGS 压缩工作多以“剪枝”为主要路线:先给每个高斯打“重要性得分”,再按阈值进行删减。这样做的坏处是容易破坏全局几何结构,导致细节丢失或形变。本文提出的 Gaussian-Herding-across-Pens (GHAP) 方法的出发点是:把整套 3DGS 看作一个高斯混合模型,用“全局最优”的方式重建一个更小的混合模型,以实现更近似的模型压缩。
高斯混合简化 (GMR) 旨在寻找一个高斯数量更小的混合分布来近似高斯数量更多的混合分布。下图中给出了一个一维分布的示例。左边8个高斯的混合分布的密度函数(实线)和右边只有3个高斯的混合分布的密度函数几乎无差异。
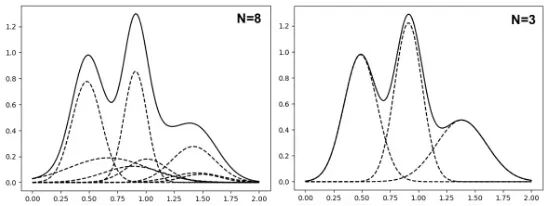
GMR 在贝叶斯滤波、机器人等领域有许多应用。本研究创新性地将3DGS原模型看作一个高斯混合模型:
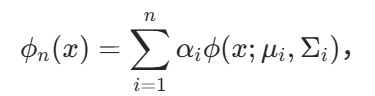
压缩后的 3DGS 对应另一个需要优化的混合模型:
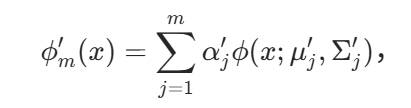
其中m远远小于n。受现有GMR技术的启发,作者通过最小化以下的复合传输散度得到压缩后的 3DGS 高斯球:
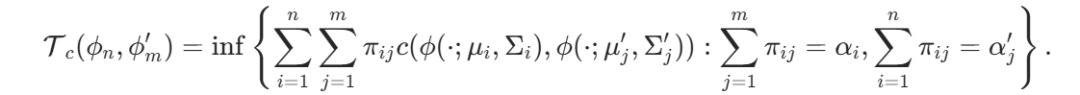
该距离受到最优传输理论的启发,将高斯混合分布看做高斯分布空间中的一个个点,并在该空间上,将这些点搬运到给定数量的新的高斯点,以此保留原高斯分布的几何结构。该算法可以被解释成一个简单的k-means求解过程。聚类中心是最终压缩得到的高斯参数。在每次迭代时,根据每一个高斯点离当前聚类中心的最近距离 (通过 c 来刻画) 将高斯点分为m个类,并在类内计算重心来更新聚类中心。为此,本文专为3DGS设计了一个简单且合适的代价函数 c,
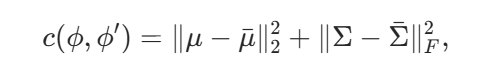
可以使得聚类中心的迭代过程如下:
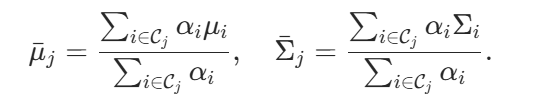
下面的例子直观地展示了GMR方法与传统的剪枝方法的差异:
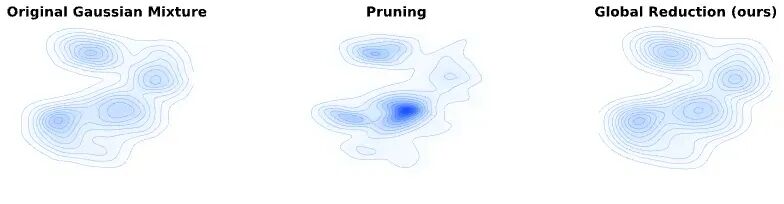
可以看到,高斯混合简化方法显著保留了概率分布的结构形态,返回到3DGS模型中,就相当于尽可能保留了原3D物体的几何形态。
由于3DGS中的高斯球数量巨多,本研究进一步设计了一个有效的3DGS压缩流程。对于使用任意3DGS及其变体训练的3DGS模型,先对它使用KD-tree进行空间划分,然后再在每个分块中运行高斯混合简化技术,得到更轻量化的3DGS模型。为了让模型适应新的结构,作者在最后加入了一个外形优化模块,继续优化除了位置和形状信息外的特征,提高新视角合成任务中的表现。整个流程就好像牧羊人将羊群赶入一个个围栏,让他们井然有序地保持固定的形态。方法流程图如下。
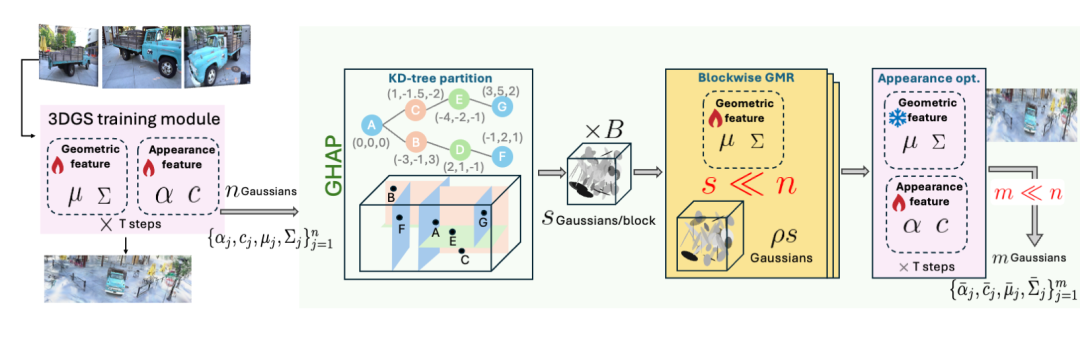
在文章中,作者与多个基于剪枝的压缩方法和端到端的压缩方法进行了比较。通过将压缩后高斯球的数量按照大小分组,我们可以观察到基于GHAP压缩后的表现领先于其他基线方法。且非常较接近全样本的端到端方法。
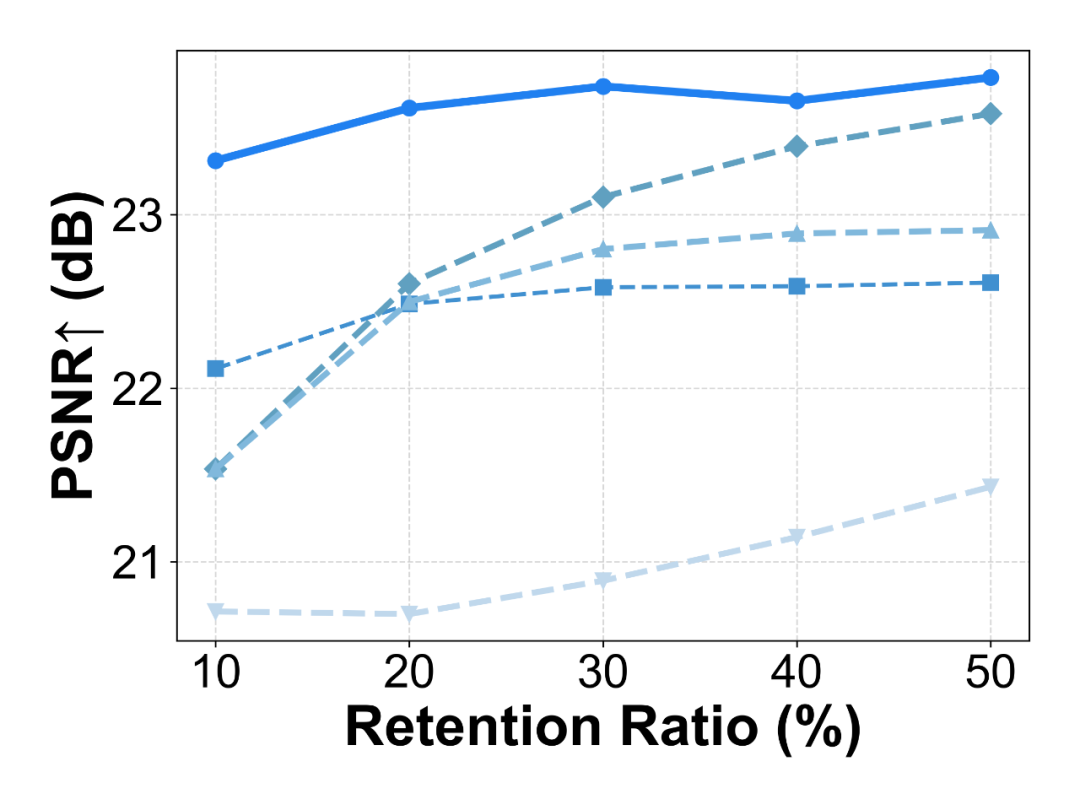
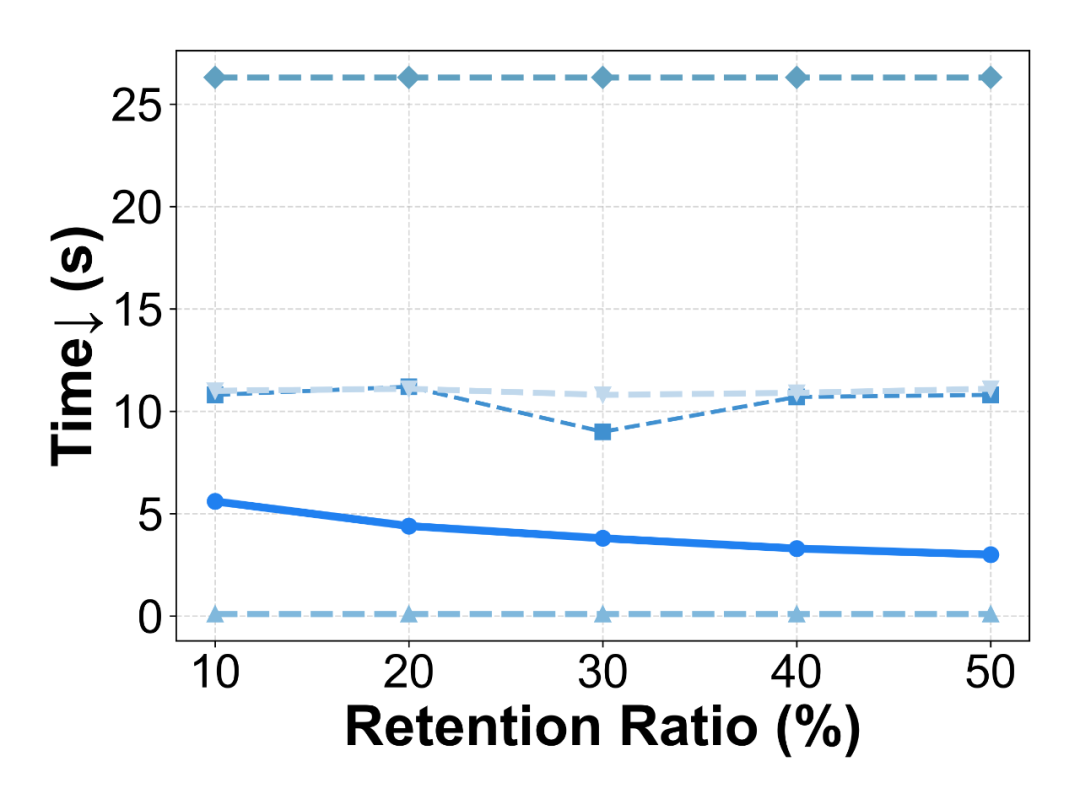
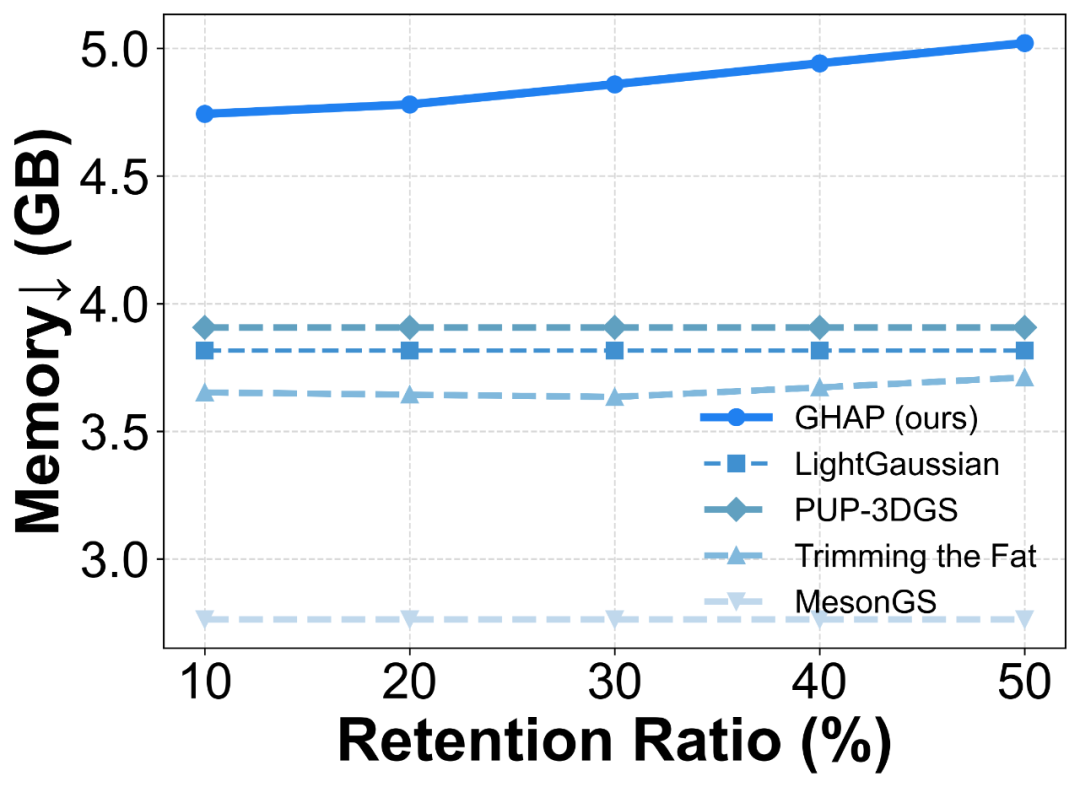
RD图结果也显示,该方法一致优于其他剪枝的方法,且在时间上也有较大优势,但是内存占用会有些许提升。
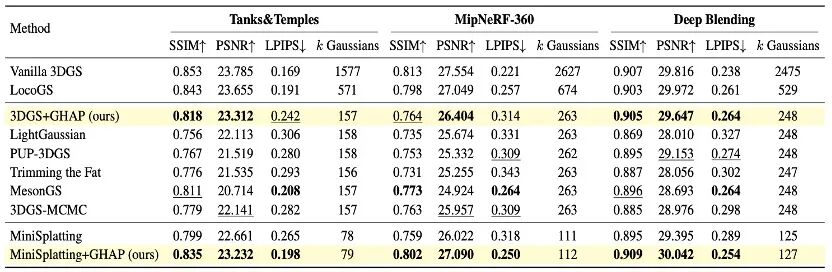
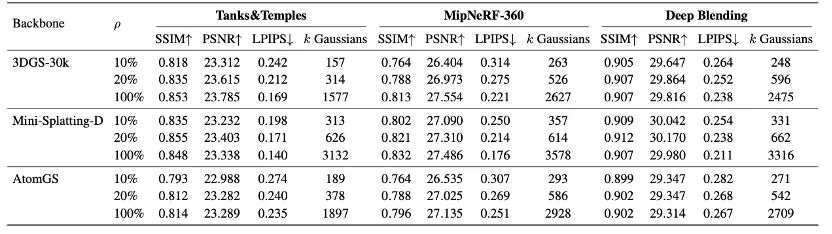
同时,本文也验证了GHAP压缩方法的可扩展性。作者将GHAP方法应用于多个不同3DGS框架中,下表结果显示,GHAP方法可以很好地保留基础模型的性能,有时甚至可以实现对基础模型表现的反超。
作者也展示了在10%的保留率下GHAP方法作用在不同基模型和不同场景上的视觉效果。在大部分场景中中,GHAP相较于未压缩模型都有极高的视觉保真度。红色圈中部分代表压缩后模型与原模型稍有肉眼可见的差异。

文章来自于微信公众号 “机器之心”,作者 “机器之心”